图像处理与分析——实验三-频率域图像增强

实验目标:
图像频域变换与滤波处理:
- 对一系列图像(1.bmp,2.bmp,2.jpg,3.bmp,4.bmp)进行傅立叶变换和离散余弦变换(DCT)以分析其频域特征。
- 使用空间域图像增强方法来增强变换后得到的频谱图。
- 应用低通和高通滤波器对图像进行频率域滤波,并通过设置不同的阈值来观察滤波效果。
频率域图像比较分析:
- 比较指定图像对(5.bmp和10.bmp,6.bmp和9.bmp,10.bmp、11.bmp和12.bmp)的频率域特征,分析不同图像在频率域的差异性,并探讨其背后的原因。
频谱图逆变换的优化学习实验:
- 使用PyTorch实现离散傅里叶逆变换,并将频谱图的初始值设为高斯噪声的模型参数。
- 通过将逆变换结果与原图之间的均方误差作为损失函数,对模型参数进行优化,验证是否能够通过优化学习到精确的频谱图。
一、
实验要求:
1.用Python写程序,对目录下的图像(1.bmp,2.bmp,2.jpg,3.bmp,4.bmp),实现:
①查看不同图像的傅立叶变换的图像
②查看不同图像的DCT(离散余弦)变换
③对变换后得到的频谱图使用空间域图像增强的方法增强效果
④采用低通滤波器和高通滤波器对图像进行频率域滤波,设置不同的阈值,查看效果
实验图片路径为: imgs/1.bmp
输出路径为:outputs/
请按照exp3_1_i的格式,输出每个任务结果
实验方案:
在实验一中,我探索了图像的频域特性,应用了傅立叶变换、离散余弦变换(DCT)、频谱图增强,以及低通和高通滤波器的技术。下面将详细解释每个步骤的关键代码及其功能:
图像加载与预处理
首先,使用load_images函数从指定文件夹加载图像集。这个函数读取图像为灰度格式,便于后续的频域处理。每个图像文件名通过替换.为_生成一个唯一标识符,用于保存处理后的结果。
1 | def load_images(folder): |
傅立叶变换
使用apply_fourier_transform函数对图像执行傅立叶变换,该函数通过numpy.fft库计算二维傅立叶变换,将频率为0的分量移到频谱中心,并通过对数变换增强结果的可视化。
1 | def apply_fourier_transform(image): |
离散余弦变换(DCT)
在apply_dct函数中,图像首先被裁剪为偶数尺寸以适应DCT要求,然后应用DCT变换。结果被归一化和调整以便于显示。
1 | def apply_dct(image): |
频谱图增强
enhance_spectrum函数通过对频谱图进行对数变换来增强其视觉表现,使得高频和低频成分的差异更加明显。
1 | def enhance_spectrum(spectrum): |
滤波器应用
apply_filter函数允许应用低通或高通滤波器。通过创建一个中心为1的二值掩模(对于低通滤波器)或其补集(对于高通滤波器),实现对频谱的选择性保留或剔除。
1 | def apply_filter(image, low_pass=True, cutoff=30): |
图像处理与保存
在process_and_save_image函数中,我将上述所有处理步骤集成在一起,对每幅图像依次执行傅立叶变换、DCT变换、频谱增强、高通和低通滤波,然后将处理结果并排显示并保存。
1 | def process_and_save_image(img, title, filename): |
实验结果:
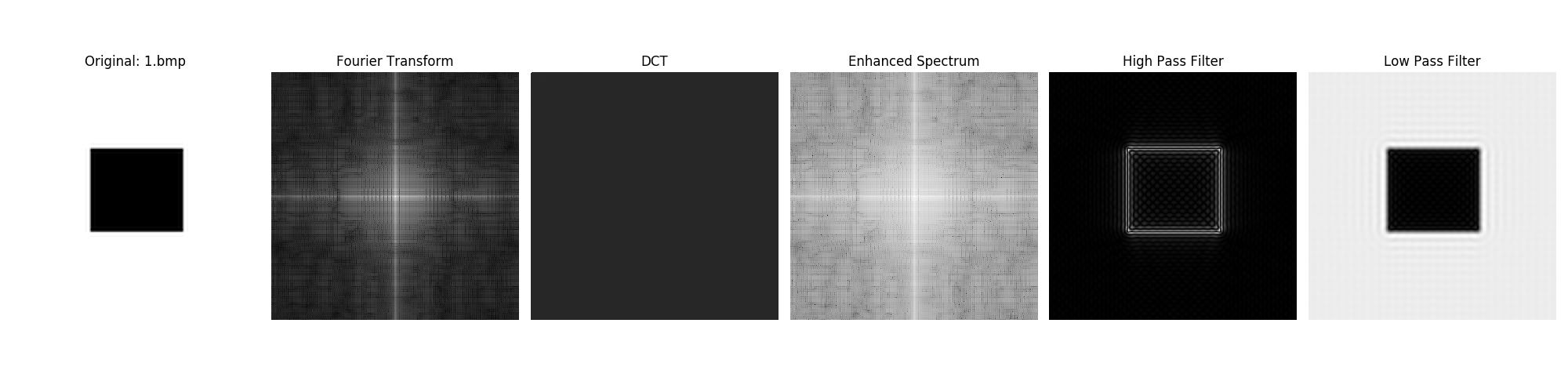




**傅立叶变换 (FT)**:
- 傅立叶变换揭示了图像的频率成分。中心的亮点表明了低频成分的集中,这在结构简单且对称的图像中更为明显。在傅立叶图像中观察到的模式直接关联到原始图像的空间复杂度。
**离散余弦变换 (DCT)**:
- DCT主要用于图像压缩中,其转换结果通常不如傅立叶变换直观。DCT图像中暗部较多,因为它集中表示了图像中的能量,并且能量大部分集中在变换的左上角,对于自然图像和复杂图案来说尤其明显。
增强频谱图:
- 频谱图经过对数变换后,细节更加明显。这种增强有助于分析图像的频率成分,特别是在进行噪声分析和滤波设计时。
高通滤波器:
- 高通滤波器用于突出图像中的高频细节,如边缘和细微纹理。处理后的图像显示了边缘增强的效果,特别是在复杂图案和自然场景中,高频细节被强化,而低频背景信息则被抑制。
低通滤波器:
- 低通滤波器主要用于平滑图像,减少高频噪声。应用低通滤波后的图像显示出更平滑的外观,图像的粗糙边缘和高频噪点得到了有效抑制,适用于去噪和图像去细节化处理。
这些结果清晰地展示了各种频率域处理技术对图像特性的影响,每种处理方法针对不同的应用场景和需求有其独特的优势和局限。通过这些实验,我可以更深入地理解和利用这些技术来改善图像分析和处理的效果。
二、
实验要求:
2.比较5.bmp和10.bmp,6.bmp和9.bmp,10.bmp、11.bmp和12.bmp 频率域图像的不同,说明原因
实验图片路径为: imgs/
输出路径为:outputs/
请按照exp3_2_i的格式,输出结果
实验方案:
任务2主要集中在比较不同图像对的频率域特征。这里的目的是探讨不同图像在频率域的差异性,并尝试从中分析原因。这些分析有助于我理解图像内容与其频率成分之间的关系。下面是关键代码的解释和分析,以及如何用它来执行实验:
图像加载与预处理
使用load_image函数从指定路径加载图像,并转换为灰度格式,这是进行频率域分析的基础。这一步骤确保了处理的统一性和准确性。
1 | def load_image(image_path): |
傅立叶变换
通过fourier_transform函数对图像执行傅立叶变换,以获取其频率域表示。这个函数不仅应用了FFT来转换图像,还通过对数变换增加了频谱的对比度,使得高频和低频成分更易于区分。
1 | def fourier_transform(image): |
频率域特征比较
compare_frequency_domain函数用于比较两幅图像的频率域特征。函数首先对每幅图像应用傅立叶变换,然后在一个画布上并排显示每幅图像的原始和频率域图像。这种可视化有助于直观地比较两幅图像在频率成分上的异同。
1 | def compare_frequency_domain(image_path1, image_path2, output_filename): |
实验结果:




红色部分:这通常代表频谱图中的主要频率成分,即图像中最强烈的周期性结构。在具有清晰方向性条纹的图像中,如水平或垂直条纹,红色亮点或线通常沿着频谱中心线出现,指示了这些条纹的方向和间隔。红色亮点越明显,表示该方向上的周期性结构越规则和显著。
黄色部分:黄色通常表示频谱中的次级频率成分,它们可能不如主要成分(红色)强烈,但仍然标志着图像中的重要周期性特征。在斜条纹或更复杂图案的图像中,黄色亮线或点可能呈现交叉或分布于不同的方向,表明图像具有多个主要的频率成分。
黑色背景:黑色区域表示频谱中相对较低或没有能量的区域,这表明原图在这些频率上没有明显的结构或周期性信息。这些区域的存在帮助突出了更有结构性或周期性的图像特征。
这些频率域的图像清晰地展示了图像结构的方向性特征如何影响其频谱表示:
- 水平或垂直条纹主要在垂直或水平方向上产生亮线。
- 条纹的密集程度影响频率域中亮线的分散程度。
- 斜向条纹导致频率域中多方向的亮线交叉,表明图像具有多个主要方向的频率成分。
通过这些实验,可以更深入地理解图像内容与其频率特性之间的关系,为图像分析和处理提供了有力的视觉和定量工具。这种分析特别有助于在图像处理和机器视觉应用中设计更有效的滤波和图像识别算法。
三、
实验要求:
3.通过离散傅里叶变换我可以得到频谱图,通过离散傅里叶逆变换我可以将频谱图转换为原图,请使用pytorch实现离散傅里叶逆变换(可使用库函数或自定义函数),并将频谱图设置为初始值为高斯噪声的模型参数,利用逆变换的结果与原图之间的均方误差作为损失函数对模型参数进行优化,验证是否能够通过优化学习到频谱图。
实验图片路径为:imgs/2.JPG
输出路径为:outputs/
请按照exp3_3_i的格式,输出结果
实验方案:
任务3的目的是通过离散傅里叶逆变换(IDFT)从频谱图重建图像,并使用机器学习技术优化重建过程。该任务利用PyTorch框架进行实现,以下是关键代码的逐步分析和对应的实验过程解释:
图像加载与预处理
使用load_image函数加载图像并将其转换为灰度格式,这是进行频域操作的标准准备步骤。转换为灰度是因为颜色信息在此类任务中通常不是必需的,而且灰度化简化了数据处理。
1 | def load_image(image_path): |
频谱参数初始化
init_params函数初始化频谱的实部和虚部参数,这些参数将被视为需要优化的模型参数。使用标准正态分布进行初始化是一种常见的做法,可以帮助加速优化过程。
1 | def init_params(shape): |
离散傅里叶逆变换
inverse_fft函数将初始化的频谱参数(实部和虚部)合成复数,并执行逆傅立叶变换。这个逆变换的目的是从频谱图重建出原始图像。
1 | def inverse_fft(real, imag): |
优化与训练过程
在main函数中,设置了模型训练的各个阶段,包括损失函数的定义、优化器的配置以及学习率调度器的设置。损失函数使用均方误差(MSE),优化器使用Adam,这两者都是处理此类问题的常见选择。
1 | def main(): |
在这个过程中,每500次迭代记录一次重建的图像状态,以便可视化和评估模型的性能。这种定期记录的方法有助于监控重建过程的进展和效果。
1 | if epoch % 500 == 0: |
结果可视化与保存
最后,通过matplotlib绘制原始图像、中间过程图和最终重建图像,展示了从初始化的高斯噪声到接近原始图像的逐步重建过程。
1 | titles = ['Original', 'Intermediate', 'Final Reconstruction'] |
实验结果:

- 原始图像:
- 这是重建任务的基准图像,用作损失函数计算的参考。
- 中间重建(1500次迭代):
- 在1500次迭代后的图像显示了重建过程的中间阶段。此时的图像还包含大量的噪声和不清晰的细节,说明重建过程尚未完成,但重建的主体结构开始变得可辨认。
- 最终重建(2000次迭代):
- 经过2000次迭代,图像的重建质量显著提高。比较中间和最终重建图像,可以看到细节更加清晰,噪声大幅减少。这表明优化过程有效地调整了频谱参数,逐渐接近原始图像的质量。
技术细节与优化过程
- 损失函数:使用均方误差(MSE)来量化重建图像与原始图像之间的差异。MSE提供了一个量化的衡量标准,用于评估图像质量和指导参数的优化。
- 优化器与学习率调度:使用Adam优化器因其适应性高,能够自动调整每个参数的学习率。配合学习率调度器,系统能够在训练过程中调整学习速率,帮助优化过程在初期快速收敛,在后期稳定细化。
- 实部与虚部参数:初始设定为正态分布的随机数,这种随机初始化方法有助于破坏初始的结构偏见,允许算法在重建过程中自由探索空间,寻找最佳解。
实验总结:
在本次实验中,我深入探讨了图像处理中的频率域技术。实验目标是通过对图像进行频域变换和滤波处理,以及通过优化技术重新学习图像的频谱图,来增强图像质量和理解图像内容。
实验一的关键发现:
- 傅立叶变换和DCT变换有效地揭示了图像的频率成分,其中傅立叶变换提供了全面的频率信息,而DCT更适用于压缩和编码应用。
- 通过增强处理的频谱图在视觉上更易于分析,尤其是对于识别图像中的主要频率成分。
- 低通和高通滤波器的应用展示了如何通过频率域处理来平滑图像或增强图像边缘。
实验二的关键发现:
- 不同图像对的频率域特征比较揭示了图像间的明显差异,这些差异通常与图像的细节和纹理复杂度相关。
- 高频成分的分布与图像内容的复杂性和边缘信息密切相关,而低频成分则与图像的整体形状和结构特征相关。
实验三的关键发现:
- 离散傅里叶逆变换实验显示,通过优化可以从初始化的高斯噪声中学习到精确的频谱图,从而重建与原图非常接近的图像。
- 该过程验证了频谱图中包含的丰富信息和通过逆变换重建图像的可行性。
总之,这一系列实验不仅增强了我的图像处理技能,特别是在频率域分析和处理方面,还加深了我对图像结构和内容如何影响其频率特性的理解。
- Title: 图像处理与分析——实验三-频率域图像增强
- Author: ELecmark
- Created at : 2024-04-29 11:00:07
- Updated at : 2024-05-11 12:13:23
- Link: https://elecmark.github.io/2024/04/29/图像处理与分析——实验三-频率域图像增强/
- License: This work is licensed under CC BY-NC-SA 4.0.
